Binary Indexed Tree (Fenwick Tree)

What is a Binary Indexed Tree

Binary Indexed Tree is a data structure that can store array of length with following property

• Calculates the value of function in the given range in time. There are some restriction on which kind of function you can use, for example sum function works, but min/max function don't.
• Updates the value of an element of in time
• Requires only spaces, which is the input spaces

Why do we need it

Naive calculation of in the range usually cost . Imagine you have queries, each of them traverse through an array length , you would end up having 10 billions traversal and TLE.

How it works

Here is an example of a BIT representation for an array of 8 items

<center>

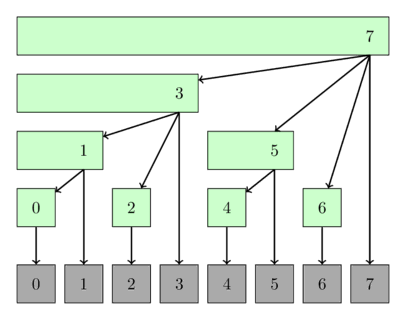<small>(image taken from cp-algorithms.com)</small>

</center>

In this example, let be the original array and be the BIT version of . Let be the sum function for the sake of simplicity.

Here is the process to calculate

1. Start with , covers only , we add the the final result
2. Next, we want to go to the next uncovered range, which is , covers , we add to the final result
3. Next uncovered range, . covers . Add to the final result. We end here because we have covered the range .

What if you want to calculate

1. Start with , covers , we add to the final result
2. Next, we want to go to the next uncovered range, which is . covers . Add to the final result and we are done.

What if you want to calculate

1. Start with , Luckily enough, covers so we already got the answer, which is

Definition of

The computation of   is defined using the following simple operation: we replace all trailing 1 bits in the binary representation of   with 0 bits.

In other words, if the least significant digit of   in binary is 0, then  . And otherwise the least significant digit is a 1, and we take this 1 and all other trailing 1s and flip them.

There exists a simple implementation of using bitwise operator as follow

Example of

It means will be covering

It means will be respectively covering only

C++ implementation

BIT 1D

struct FenwickTree {
    vector<int> bit;  // binary indexed tree
    int n;

    FenwickTree(int n) {
        this->n = n;
        bit.assign(n, 0);
    }

    int sum(int r) {
        int ret = 0;
        for (; r >= 0; r = (r & (r + 1)) - 1)
            ret += bit[r];
        return ret;
    }

    int sum(int l, int r) {
        return sum(r) - sum(l - 1);
    }

    void add(int idx, int delta) {
        for (; idx < n; idx = idx | (idx + 1))
            bit[idx] += delta;
    }
};

BIT 2D

struct FenwickTree2D {
    vector<vector<int>> bit;
    int n, m;

    // init(...) { ... }

    int sum(int x, int y) {
        int ret = 0;
        for (int i = x; i >= 0; i = (i & (i + 1)) - 1)
            for (int j = y; j >= 0; j = (j & (j + 1)) - 1)
                ret += bit[i][j];
        return ret;
    }

    void add(int x, int y, int delta) {
        for (int i = x; i < n; i = i | (i + 1))
            for (int j = y; j < m; j = j | (j + 1))
                bit[i][j] += delta;
    }
};

Learn more

See this for more detailed explaination: https://cp-algorithms.com/data_structures/fenwick.html