Increment Submatrices by One

Problem

You are given a positive integer $n$, indicating that we initially have an $n \times n$ 0-indexed integer matrix $mat$ filled with zeroes.

You are also given a 2D integer array $query$. For each $query_i = [row1_i, col1_i, row2_i, col2_i]$, you should do the following operation:

• Add $1$ to every element in the submatrix with the top left corner $(row1_i, col1_i)$ and the bottom right corner $(row2_i, col2_i)$.
• That is, add $1$ to $mat[x][y]$ for for all $row1_i \leq x \leq row2_i$ and $col1_i \leq y \leq col2_i$.

Return the matrix $mat$ after performing every query.

Example

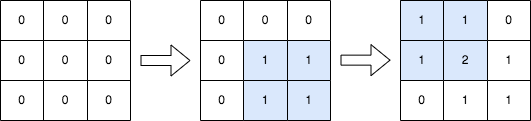
Input: n = 3, queries = [[1,1,2,2],[0,0,1,1]]
Output: [[1,1,0],[1,2,1],[0,1,1]]
Explanation: The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).

Input: n = 2, queries = [[0,0,1,1]]
Output: [[1,1],[1,1]]
Explanation: The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.

Constraints

• $1 \leq n \leq 500$
• $1 \leq queries.length \leq 104$
• $0 \leq row1_i \leq row2_i < n$
• $0 \leq col1_i \leq col2_i < n$

Submit your solution at here

Solution

Brute Force (TLE)

The brute force approach has $O(m \times n^2)$ complexity and very likely to TLE. But I heard some people managed to AC with it. I was not that lucky and got TLE.

class Solution {
public:
    vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) {
        vector<vector<int>> ret(n, vector<int>(n, 0));
        for(auto& q: queries) {
            for(int i = q[0];i<=q[2];i++)
                for(int j = q[1];j<=q[3];j++)
                    ret[i][j]++;
        }
        return ret;
    }
};

Intuition

We will solve this row by row. On each row, we manage an array $delta$ to keep track of how the value change. Let $delta_i = k$ denotes that $ans_i = ans_{i-1}+k$ For each query $q$ that span from $[a,b]$ it will make $delta_a = delta_a + 1$ and $delta_{b+1} = delta_{b+1} - 1$, everything in the middle would not change and stay as is. We can build the $delta$ array in $O(m \times n)$ where $m$ is the $queries.length$. We also need a nested loop to update the array so the overall complexity would be $O(m \times n+n^2)$

Complexity

• Time complexity: $O(m \times n+n^2)$
• Space complexity: $O(n^2)$

Code

class Solution {
public:
    vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) {
        vector<vector<int>> ret(n, vector<int>(n, 0));
        vector<vector<int>> delta(n, vector<int>(n, 0));
        for(auto& q: queries) {
            int x0 = q[0], y0 = q[1], xn = q[2], yn = q[3];
            for(int y = y0;y<=yn;y++) {
                delta[x0][y]++;
                if(xn+1 >= n) continue;
                delta[xn+1][y]--;
            }
        }
        for(int x = 0;x<n;x++) {
            for(int y = 0;y<n;y++) {
                auto prev = (x == 0?0:ret[x-1][y]);
                ret[x][y] = prev + delta[x][y];
            }
        }
        return ret;
    }
};

FYI

I failed today’s contest 😭😭😭 There goes my rating.