K Radius Subarray Averages
Problem
You are given a 0-indexed array of integers, and an integer .
The -radius average for a subarray of centered at some index with the radius is the average of all elements in between the indices and (inclusive). If there are less than elements before or after the index , then the -radius average is .
Build and return an array of length where is the -radius average for the subarray centered at index .
The average of elements is the sum of the elements divided by , using integer division. The integer division truncates toward zero, which means losing its fractional part.
For example, the average of four elements 2, 3, 1, and 5 is (2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75, which truncates to 2.
Example
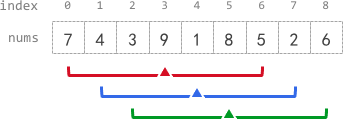
Input: nums = [7,4,3,9,1,8,5,2,6], k = 3
Output: [-1,-1,-1,5,4,4,-1,-1,-1]
Explanation:
- avg[0], avg[1], and avg[2] are -1 because there are less than k elements before each index.
- The sum of the subarray centered at index 3 with radius 3 is: 7 + 4 + 3 + 9 + 1 + 8 + 5 = 37.
Using integer division, avg[3] = 37 / 7 = 5.
- For the subarray centered at index 4, avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4.
- For the subarray centered at index 5, avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4.
- avg[6], avg[7], and avg[8] are -1 because there are less than k elements after each index.
Input: nums = [100000], k = 0
Output: [100000]
Explanation:
- The sum of the subarray centered at index 0 with radius 0 is: 100000.
avg[0] = 100000 / 1 = 100000.
Input: nums = [8], k = 100000
Output: [-1]
Explanation:
- avg[0] is -1 because there are less than k elements before and after index 0.
Constraints
Submit your solution at here
Solution
Approach
There are many ways to solve this:
- We can do full scan from to and calculate average of each position
- Or we can slide over that windows, remove left most item and add right most item, then update the average
- Or we can calculate prefix sum of , then for each position, we query the sum of range using that prefix sum
Complexity
- Time complexity: , , respectively
- Space complexity: , , respectively
- Surprisingly all approach AC, normally doesn't work well with
Code
solution
use std::iter;
impl Solution {
pub fn get_averages(nums: Vec<i32>, k: i32) -> Vec<i32> {
let k = k as usize;
let n = nums.len();
let m = k*2+1;
if n < m {
return vec![-1;n];
}
let avg: Vec<i32> = nums.windows(m)
.map(|a| a.iter().fold(0, |acc, &x| acc + x as i64))
.map(|x| (x/m as i64) as i32)
.collect();
let left = iter::repeat(-1)
.take(k);
let right = left.clone();
left.chain(avg.into_iter())
.chain(right)
.collect()
}
}
Sliding window solution
impl Solution {
pub fn get_averages(nums: Vec<i32>, k: i32) -> Vec<i32> {
let k = k as usize;
let n = nums.len();
let m = k*2+1;
let mut ret = vec![-1;n];
if n < m {
return ret;
}
let mut acc = nums.iter()
.take(m)
.fold(0, |acc, &x| acc + x as i64);
let m = m as i64;
ret[k] = (acc/m) as i32;
for i in k+1..n-k {
acc -= nums[i-k-1] as i64;
acc += nums[i+k] as i64;
ret[i] = (acc/m) as i32;
}
ret
}
}
Prefix sum solution
impl Solution {
pub fn get_averages(nums: Vec<i32>, k: i32) -> Vec<i32> {
let k = k as usize;
let n = nums.len();
let m = k*2+1;
let mut ret = vec![-1;n];
if n < m {
return ret;
}
let mut prefix = vec![0;n+1];
for i in 1..=n {
prefix[i] = prefix[i-1] + nums[i-1] as i64;
}
for i in k..n-k {
let x = prefix[i+k+1] - prefix[i-k];
ret[i] = (x/m as i64) as i32;
}
ret
}
}