Maximum Strictly Increasing Cells in a Matrix

Problem

Given a 1-indexed $m \times n$ integer matrix $mat$, you can select any cell in the matrix as your starting cell.

From the starting cell, you can move to any other cell in the same row or column, but only if the value of the destination cell is strictly greater than the value of the current cell. You can repeat this process as many times as possible, moving from cell to cell until you can no longer make any moves.

Your task is to find the maximum number of cells that you can visit in the matrix by starting from some cell.

Return an integer denoting the maximum number of cells that can be visited.

Example

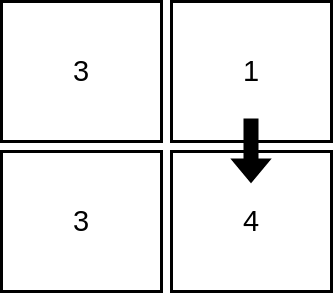
Input: mat = [[3,1],[3,4]]
Output: 2
Explanation: The image shows how we can visit 2 cells starting from row 1, column 2. It can be shown that we cannot visit more than 2 cells no matter where we start from, so the answer is 2.

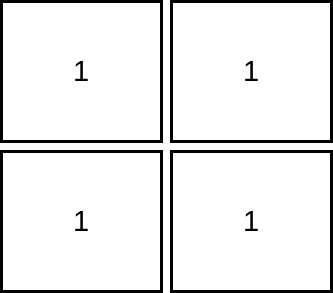
Input: mat = [[1,1],[1,1]]
Output: 1
Explanation: Since the cells must be strictly increasing, we can only visit one cell in this example.

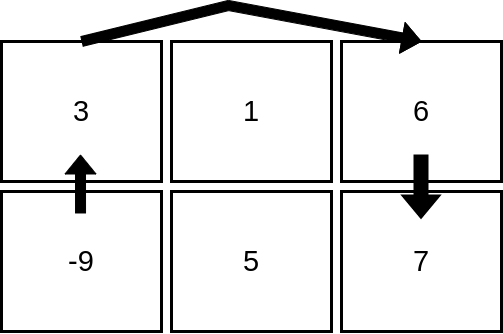
Input: mat = [[3,1,6],[-9,5,7]]
Output: 4
Explanation: The image above shows how we can visit 4 cells starting from row 2, column 1. It can be shown that we cannot visit more than 4 cells no matter where we start from, so the answer is 4.

Constraints

• $1 \leq m,n \leq 10^5$
• $1 \leq m \times n \leq 10^5$
• $-10^5 \leq mat_{i,j} \leq 10^5$

Submit your solution at here

Solution

Approach

We use greedy approach here:

• Travel from low value to high value. That way we can easily update new max score by taking previous max score and increase by 1
• Keep track of maximum score in a each row and column with 2 array best_row and best_column

Complexity

• Time complexity: $O(nm \times log(nm))$
• Space complexity: $O(nm)$

Code

use std::collections::BinaryHeap;
use std::cmp::max;
impl Solution {
    pub fn max_increasing_cells(mat: Vec<Vec<i32>>) -> i32 {
        let n = mat.len();
        let m = mat[0].len();
        let mut ret = 1;
        let mut q = BinaryHeap::new();
        let mut best_row = vec![0;n];
        let mut best_col = vec![0;m];
        let mut next_best_row = vec![0;n];
        let mut next_best_col = vec![0;m];
        for i in 0..n {
            for j in 0..m {
                q.push((mat[i][j], i, j));
            }
        }
        let mut last_x = i32::MAX;
        let mut buffer = Vec::new();
        while let Some((x, i, j)) = q.pop() {
            if x != last_x {
                while let Some((i,j)) = buffer.pop() {
                    best_row[i] = next_best_row[i];
                    best_col[j] = next_best_col[j];
                }
            }
            next_best_row[i] = max(next_best_row[i], max(best_col[j]+1, best_row[i]+1));
            next_best_col[j] = max(next_best_col[j], max(best_row[i]+1, best_col[j]+1));
            ret = max(max(ret, next_best_row[i]), next_best_col[j]);
            last_x = x;
            buffer.push((i,j));
        }
        return ret;
    }
}