Minimum Total Distance Traveled

Problem

There are some robots and factories on the X-axis.

You are given an integer array robot where $robot_i$ is the position of the $i^{th}$ robot.

You are also given a 2D integer array $factory$ where $factory_j= (position_j, limit_j)$ indicates that $position_j$ is the position of the $j^{th}$ factory and that the $j^{th}$ factory can repair at most $limit_j$ robots.

The positions of each robot are unique. The positions of each factory are also unique. Note that a robot can be in the same position as a factory initially.

All the robots are initially broken; they keep moving in one direction.

The direction could be the negative or the positive direction of the X-axis.

When a robot reaches a factory that did not reach its limit, the factory repairs the robot, and it stops moving.

At any moment, you can set the initial direction of moving for some robot.

Your target is to minimize the total distance traveled by all the robots.

Return the minimum total distance traveled by all the robots.

The test cases are generated such that all the robots can be repaired.

Note that

• All robots move at the same speed
• If two robots move in the same direction, they will never collide
• If two robots move in opposite directions and they meet at some point, they do not collide. They cross each other
• If a robot passes by a factory that reached its limits, it crosses it as if it does not exist
• If the robot moved from a position x to a position y, the distance it moved is $|y - x|$

Example

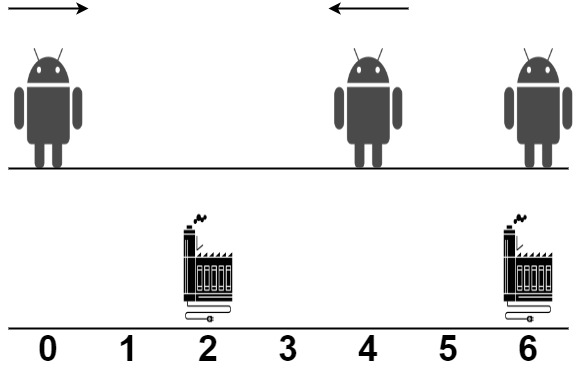
Input: robot = [0,4,6], factory = [[2,2],[6,2]]
Output: 4
Explanation: As shown in the figure:
- The first robot at position 0 moves in the positive direction. It will be repaired at the first factory.
- The second robot at position 4 moves in the negative direction. It will be repaired at the first factory.
- The third robot at position 6 will be repaired at the second factory. It does not need to move.
The limit of the first factory is 2, and it fixed 2 robots.
The limit of the second factory is 2, and it fixed 1 robot.
The total distance is |2 - 0| + |2 - 4| + |6 - 6| = 4. It can be shown that we cannot achieve a better total distance than 4.

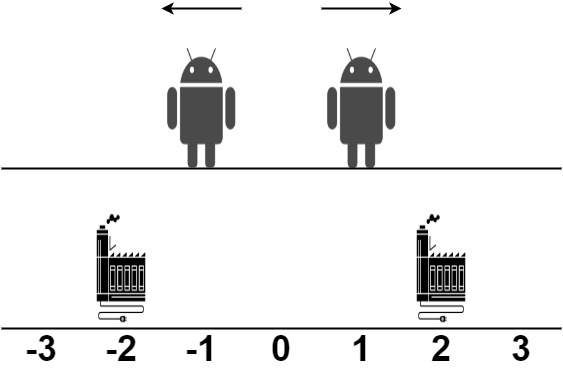
Input: robot = [1,-1], factory = [[-2,1],[2,1]]
Output: 2
Explanation: As shown in the figure:
- The first robot at position 1 moves in the positive direction. It will be repaired at the second factory.
- The second robot at position -1 moves in the negative direction. It will be repaired at the first factory.
The limit of the first factory is 1, and it fixed 1 robot.
The limit of the second factory is 1, and it fixed 1 robot.
The total distance is |2 - 1| + |(-2) - (-1)| = 2. It can be shown that we cannot achieve a better total distance than 2.

Constraints

• $1 \leq robot.length, factory.length \leq 100$
• $-10^9 \leq robot_i, position_j \leq 10^9$
• $0 \leq limit_j \leq robot.length$

Submit your solution at here

Solution

Intuition

Let $g(i,j,k)$ is the minimum distance first $i$ robots have to travel to get repaired by first $j$ factories and the last $k$ robots goes to the $j^{th}$ factory.

Let $f(i,j)$ is the minimum distance first $i$ robots have to travel to get repaired by first $j$ factories.

By that definition, $f(i,j) = min(g(i,j,k)) \quad \forall \quad k \in [0,n]$.

The answer is $f(n,m)$ where $n$ is the number of robot and $m$ is the number of factory.

Lets build the dynamic programming table calculate all $f(i,j) \quad \forall \quad i \in [1,n], j \in [1,m]$

By definition:

• $f(0, j) = 0 \quad \forall \quad j$, we need to travel 0 distance to repair 0 robot
• $f(i, 0) = \infty \quad \forall \quad i \in [1,\infty)$, we can’t repair any robot with 0 factory

Let $cost(i1,i2,j)$ is the total distance $[robot_{i1},robot_{i2}]$ has to travel to $factory_j$

Lets say we need to calculate $g(i,j,k)$, we have

$g(i,j,k) = f(i-k,j-1) + cost(i-k+1,i,j)$

Complexity

• Time complexity: $O(n^3)$
• Space complexity: $O(n^2)$, can be optimized to $O(n)$ if needed

Code

impl Solution {
    pub fn minimum_total_distance(mut robot: Vec<i32>, mut factory: Vec<Vec<i32>>) -> i64 {
        use std::cmp::min;
        robot.sort();
        factory.sort_by(|a,b| a[0].cmp(&b[0]));
        let n = robot.len();
        let m = factory.len();
        let mut f = vec![vec![0;m+1];n+1];
        for i in 1..=n {
            f[i][0] = 200_000_000_000i64;
        }
        // f[i][j] = use j factories to repair i robots, what is the minimum cost
        for i in 1..=n {
            for j in 1..=m {
                let factory_cap = factory[j-1][1];
                let factory_pos = factory[j-1][0];
                let to_repair = min(i, factory_cap as usize);
                let mut cost = 0;
                f[i][j] = f[i][j-1];
                for k in 1..=to_repair {
                    cost += (robot[i-k] - factory_pos).abs() as i64;
                    f[i][j] = min(f[i][j], f[i-k][j-1]+cost);
                }
            }
        }
        // println!("robot: {robot:?}");
        // println!("factory: {factory:?}");
        // println!("f: {f:?}");
        f[n][m]
    }
}