Sum of Distances in Tree

Problem

There is an undirected connected tree with $n$ nodes labeled from $0$ to $n - 1$ and $n - 1$ edges.

You are given the integer $n$ and the array edges where $edges_i = [a_i, b_i]$ indicates that there is an edge between nodes $a_i$ and $b_i$ in the tree.

Return an array $answer$ of length $n$ where $answer_i$ is the sum of the distances between the $i^{th}$ node in the tree and all other nodes.

Example

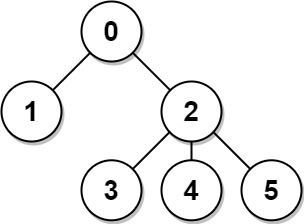
Input: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
Output: [8,12,6,10,10,10]
Explanation: The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer[0] = 8, and so on.

Input: n = 1, edges = []
Output: [0]

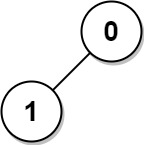
Input: n = 2, edges = [[1,0]]
Output: [1,1]

Constraints

• $1 \leq n \leq 3 \times 10^4$
• $edges.length = n - 1$
• $edges[i].length = 2$
• $0 \leq a_i, b_i < n$
• $a_i \neq b_i$

Submit your solution at here

Solution

Intuition

The first naive solution came to my mind is DFS each node and count. This brute force will result in $O(n^2)$ and obviously TLE.

But what if we have already have the answer for node $i$, can we calculate answer for all children of $i$ fast?

Approach

Actually we can do it, let’s DFS twice:

• First pass, for each node $i$ calculate sum of all path to all children of $i$
  • After first pass, the value on the root node already is the answer
• Second pass, for each node $i$ with parent $p$ that has already has answer, calculate sum of all path to the other node that on the other side (is not children) of $i$

Complexity

• Time complexity: $O(n)$
• Space complexity: $O(n)$

Code

The implementation is heavy, looks daunting but actually not too complex 😀

class Solution {
public:
    vector<int> parent;
    vector<int> childCount;
    vector<vector<int>> children;
    vector<vector<int>> adj;
    void buildTree(vector<vector<int>>& adj) {
        vector<bool> vis(parent.size(), false);
        queue<int> q;
        q.push(0);
        vis[0] = true;
        while(!q.empty()) {
            auto u = q.front();
            q.pop();
            for(auto v: adj[u]) {
                if(vis[v]) {
                    continue;
                }
                vis[v] = true;
                q.push(v);
                parent[v] = u;
                children[u].push_back(v);
            }
        }
    }
    void buildDistBottomUp(int root, vector<int>& score) {
        int p = parent[root];
        if(p != -1) {
            int n = parent.size();
            int otherSideScore = score[p] - score[root] - childCount[root] - 1;
            int otherCount = n - childCount[root] - 1;
            //cout<<"build "<<root<<" current score = "<<dist[root]<<", other side score = "<<otherSideScore<<" other count = "<<otherCount<<endl;
            score[root] += otherSideScore + otherCount;
        }
        for(auto child: children[root]) {
            buildDistBottomUp(child, score);
        }
    }
    void buildDistTopDown(int root, vector<int>& score) {
        for(auto child: children[root]) {
            buildDistTopDown(child, score);
            score[root] += score[child]+childCount[child]+1;
        }
    }
    void countChildren(int root) {
        for(auto child: children[root]) {
            countChildren(child);
            childCount[root] += childCount[child]+1;
        }
    }
    vector<int> sumOfDistancesInTree(int n, vector<vector<int>>& edges) {
        parent.resize(n,-1);
        childCount.resize(n, 0);
        children.resize(n);
        adj.resize(n);
        for(auto e: edges) {
            adj[e[0]].push_back(e[1]);
            adj[e[1]].push_back(e[0]);
        }
        vector<int> ret(n, 0);
        buildTree(adj);
        countChildren(0);
        buildDistTopDown(0, ret);
        buildDistBottomUp(0, ret);
        return ret;
    }
};